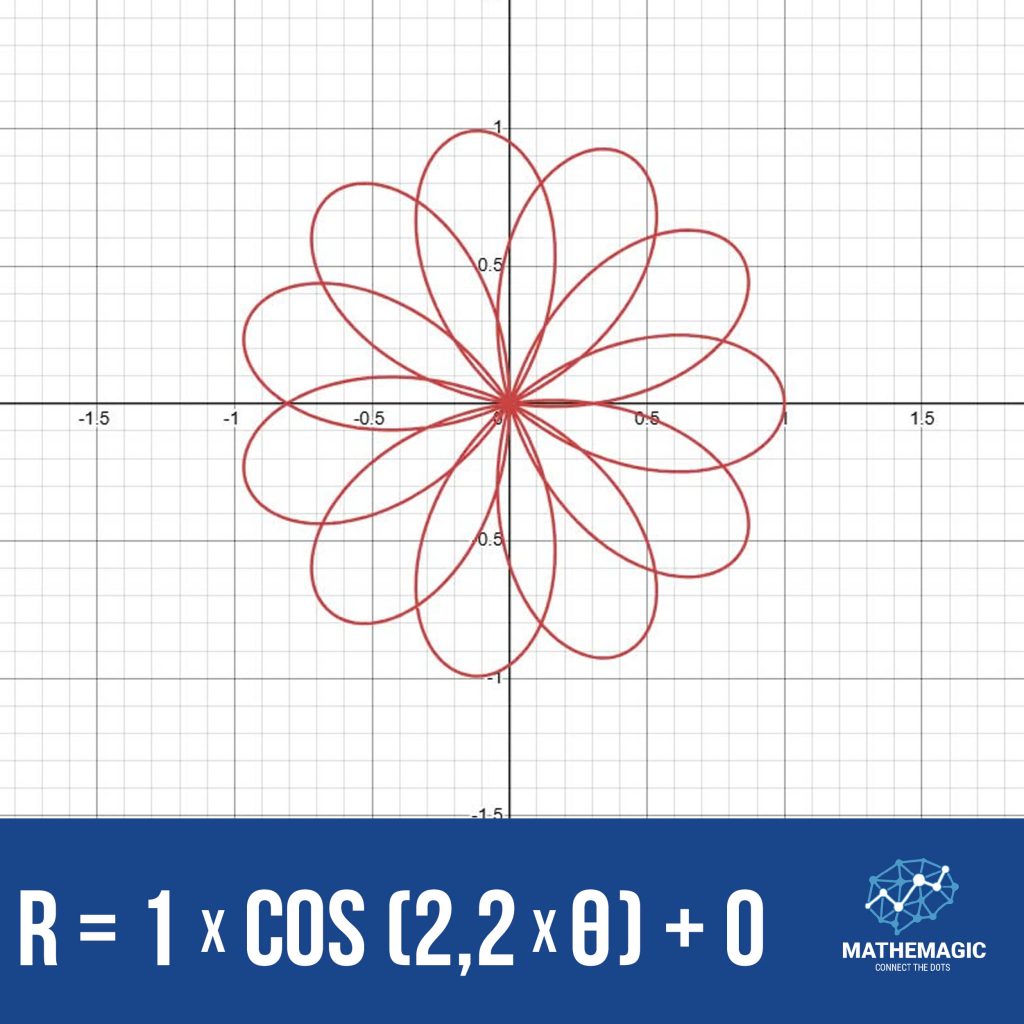
Đồ thị hình hoa, hay còn gọi là đồ thị hoa hồng (rose curve), là một loại đường cong toán học đặc biệt, có hình dạng giống như những bông hoa với nhiều cánh. Chúng được biểu diễn bằng phương trình cực
1. Khám Phá Công Thức r(t) = m * cos(t * n) + a
Công thức r(t) = m * cos(t * n) + a là một hàm số trong hệ tọa độ cực, trong đó:
• r: Bán kính của điểm trên đồ thị.
• t: Góc tạo bởi điểm đó và trục hoành.
• m: Biên độ, quyết định kích thước của cánh hoa.
• n: Số nguyên, quyết định số lượng cánh hoa.
• a: Độ dịch chuyển, quyết định vị trí tương đối của đồ thị so với tâm tọa độ.
2. Ảnh Hưởng Của Các Tham Số
• m (Biên Độ):
o “m” quyết định kích thước tổng thể của đồ thị. Khi “m” lớn, cánh hoa sẽ lớn hơn và ngược lại.
o Nếu “m” âm, đồ thị sẽ được lật ngược, tạo ra hình ảnh phản chiếu.
• n (Số Cánh Hoa):
o “n” là yếu tố quan trọng nhất quyết định số lượng cánh hoa.
o Nếu “n” là số nguyên lẻ, số cánh hoa sẽ là “n”.
o Nếu “n” là số nguyên chẵn, số cánh hoa sẽ là 2n.
o Nếu n không phải số nguyên, hình dạng sẽ trở nên rất phức tạp.
• a (Độ Dịch Chuyển):
o “a” quyết định vị trí tương đối của đồ thị so với tâm tọa độ.
o Nếu “a” lớn hơn “m”, đồ thị sẽ không có phần cánh hoa quay về tâm.
o Nếu “a” nhỏ hơn “m”, đồ thị sẽ có phần cánh hoa quay về tâm.


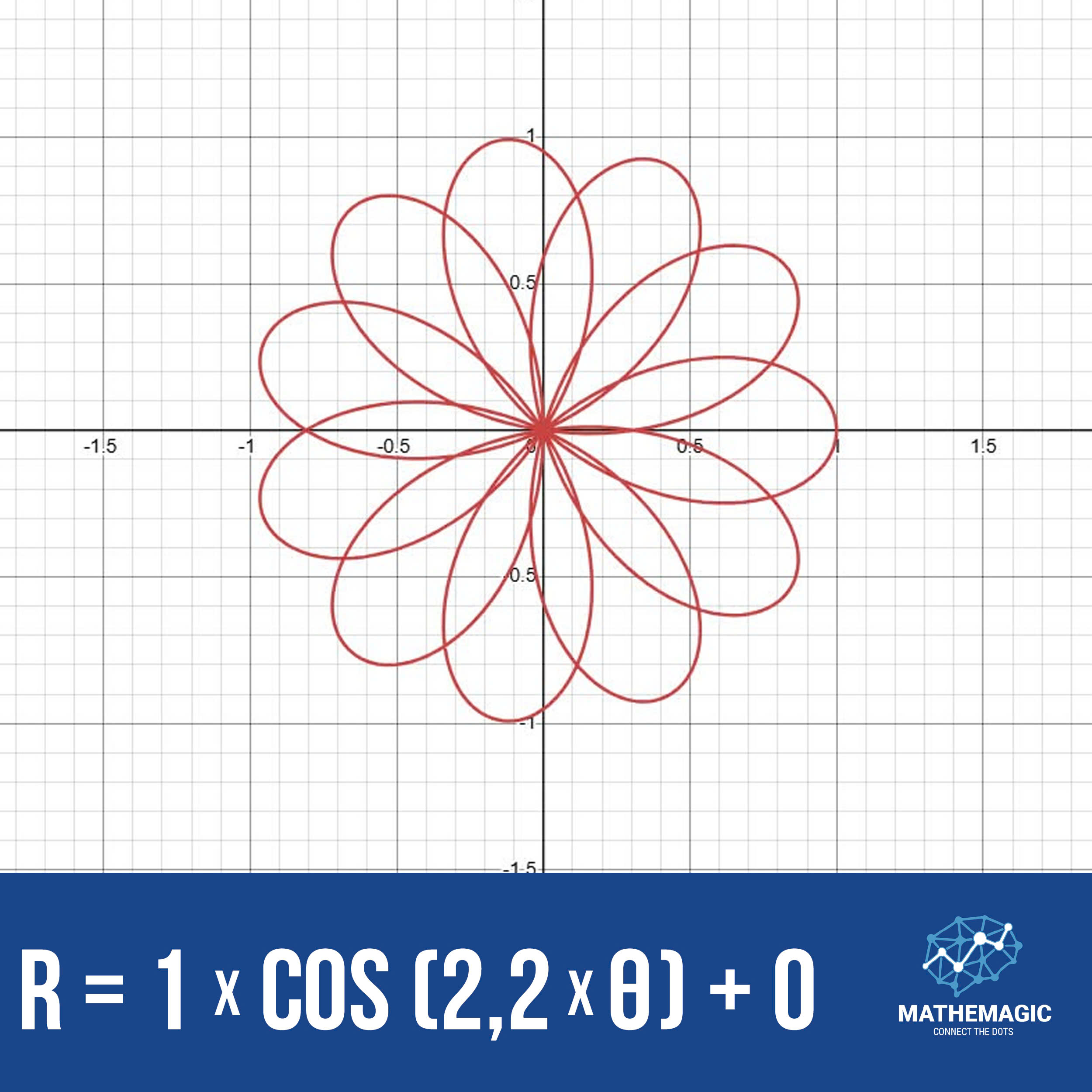
3. Vẽ Đồ Thị r(t) = m * cos(t * n) + a
Để vẽ đồ thị này, chúng ta cần sử dụng hệ tọa độ cực. Các bước thực hiện như sau:
• Chọn các giá trị cho m, n và a.
• Thay đổi giá trị của t trong một khoảng nhất định (ví dụ: từ 0 đến 2π).
• Tính toán giá trị tương ứng của r.
• Vẽ các điểm (r, t) trên hệ tọa độ cực.
• Nối các điểm lại để tạo thành đồ thị.
4. Sự Kỳ Diệu Của Hệ Tọa Độ Cực
Để vẽ đồ thị hình hoa, chúng ta sử dụng hệ tọa độ cực, một hệ tọa độ đặc biệt trong đó vị trí của một điểm được xác định bởi khoảng cách từ gốc tọa độ (bán kính “r”) và góc tạo bởi tia từ gốc tọa độ đến điểm đó và trục hoành (góc “θ”).
5. Ứng Dụng Trong Nghệ Thuật Và Thiết Kế
Vẻ đẹp của đồ thị hình hoa không chỉ giới hạn trong thế giới toán học, mà còn được ứng dụng rộng rãi trong nghệ thuật và thiết kế. Chúng xuất hiện trong:
• Thiết kế đồ họa: Tạo ra các họa tiết độc đáo và ấn tượng.
• Thiết kế thời trang: In trên vải, tạo ra những bộ trang phục mang tính nghệ thuật cao.
• Kiến trúc: Sử dụng trong thiết kế cửa sổ, lan can, tạo điểm nhấn cho công trình.
6. Kết Luận
Đồ thị hình hoa là một minh chứng tuyệt vời cho sự kết hợp giữa toán học và nghệ thuật. Chúng không chỉ là những hình dạng đẹp mắt, mà còn là những tác phẩm nghệ thuật được tạo ra từ những con số và phương trình. Hãy cùng nhau khám phá vẻ đẹp tiềm ẩn của đồ thị hình hoa và khơi nguồn sáng tạo của bản thân.