Chào mừng các bạn đến với hành trình khám phá thế giới hình học phẳng, nơi chúng ta sẽ cùng nhau tìm hiểu về các loại tứ giác khác nhau. Tứ giác là một hình đa giác có bốn cạnh và bốn góc. Chúng ta sẽ cùng nhau phân loại các tứ giác dựa trên các đặc điểm và tính chất của chúng.
- Tứ giác (Quadrilateral): Nền tảng của Thế giới Hình học Phẳng
Tứ giác là một hình đa giác cơ bản, là nền tảng để xây dựng nên các hình học phức tạp hơn. Tứ giác có nhiều hình dạng và kích thước khác nhau. Để hiểu rõ hơn về tứ giác, chúng ta cần nắm vững các khái niệm cơ bản sau:
- Cạnh (Side): Là đoạn thẳng nối hai đỉnh liên tiếp của tứ giác.
- Góc (Angle): Là phần mặt phẳng được tạo bởi hai cạnh liên tiếp của tứ giác.
- Đỉnh (Vertex): Là điểm giao nhau của hai cạnh của tứ giác.
- Đường chéo (Diagonal): Là đoạn thẳng nối hai đỉnh không liên tiếp của tứ giác.
- Tổng các góc trong của tứ giác: Luôn bằng 360 độ.
- Các Loại Tứ giác Đặc biệt: Hành trình Khám phá Sự Đa dạng
Từ tứ giác cơ bản, chúng ta có thể phân loại thành các loại tứ giác đặc biệt dựa trên các đặc điểm và tính chất của chúng. Dưới đây là một số loại tứ giác đặc biệt phổ biến:
2.1. Hình thang (Trapezoid): Sự Song song trong Hình học Phẳng
- Định nghĩa: Hình thang là tứ giác có ít nhất một cặp cạnh đối diện song song.
- Các loại hình thang:
- Hình thang thường: Chỉ có một cặp cạnh đối diện song song.
- Hình thang cân: Là hình thang có hai cạnh bên không song song bằng nhau.
- Hình thang vuông: Là hình thang có một góc vuông.
- Tính chất:
- Hai cạnh đáy song song.
- Hai góc kề một cạnh bên bù nhau.
- Trong hình thang cân, hai góc kề một đáy bằng nhau.
- Trong hình thang cân, hai đường chéo bằng nhau.
2.2. Hình bình hành (Parallelogram): Sự Cân bằng trong Hình học Phẳng
- Định nghĩa: Hình bình hành là tứ giác có hai cặp cạnh đối diện song song.
- Tính chất:
- Các cạnh đối diện song song và bằng nhau.
- Các góc đối diện bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
2.3. Hình chữ nhật (Rectangle): Sự Hoàn hảo của Các Góc Vuông
- Định nghĩa: Hình chữ nhật là hình bình hành có bốn góc vuông.
- Tính chất:
- Tất cả các tính chất của hình bình hành.
- Bốn góc vuông.
- Hai đường chéo bằng nhau.
2.4. Hình thoi (Rhombus): Sự Cân bằng của Các Cạnh Bằng Nhau
- Định nghĩa: Hình thoi là hình bình hành có bốn cạnh bằng nhau.
- Tính chất:
- Tất cả các tính chất của hình bình hành.
- Bốn cạnh bằng nhau.
- Hai đường chéo vuông góc với nhau và là đường phân giác của các góc của hình thoi.
2.5. Hình vuông (Square): Sự Kết hợp Hoàn hảo của Hình chữ nhật và Hình thoi
- Định nghĩa: Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
- Tính chất:
- Tất cả các tính chất của hình chữ nhật và hình thoi.
- Bốn cạnh bằng nhau.
- Bốn góc vuông.
- Hai đường chéo bằng nhau, vuông góc với nhau và là đường phân giác của các góc của hình vuông.
2.6. Hình cánh diều (Kite): Sự Đối xứng trong Hình học Phẳng
- Định nghĩa: Hình cánh diều là tứ giác có hai cặp cạnh kề bằng nhau.
- Tính chất:
- Hai cặp cạnh kề bằng nhau.
- Một đường chéo là đường trung trực của đường chéo còn lại.
- Một cặp góc đối diện bằng nhau.
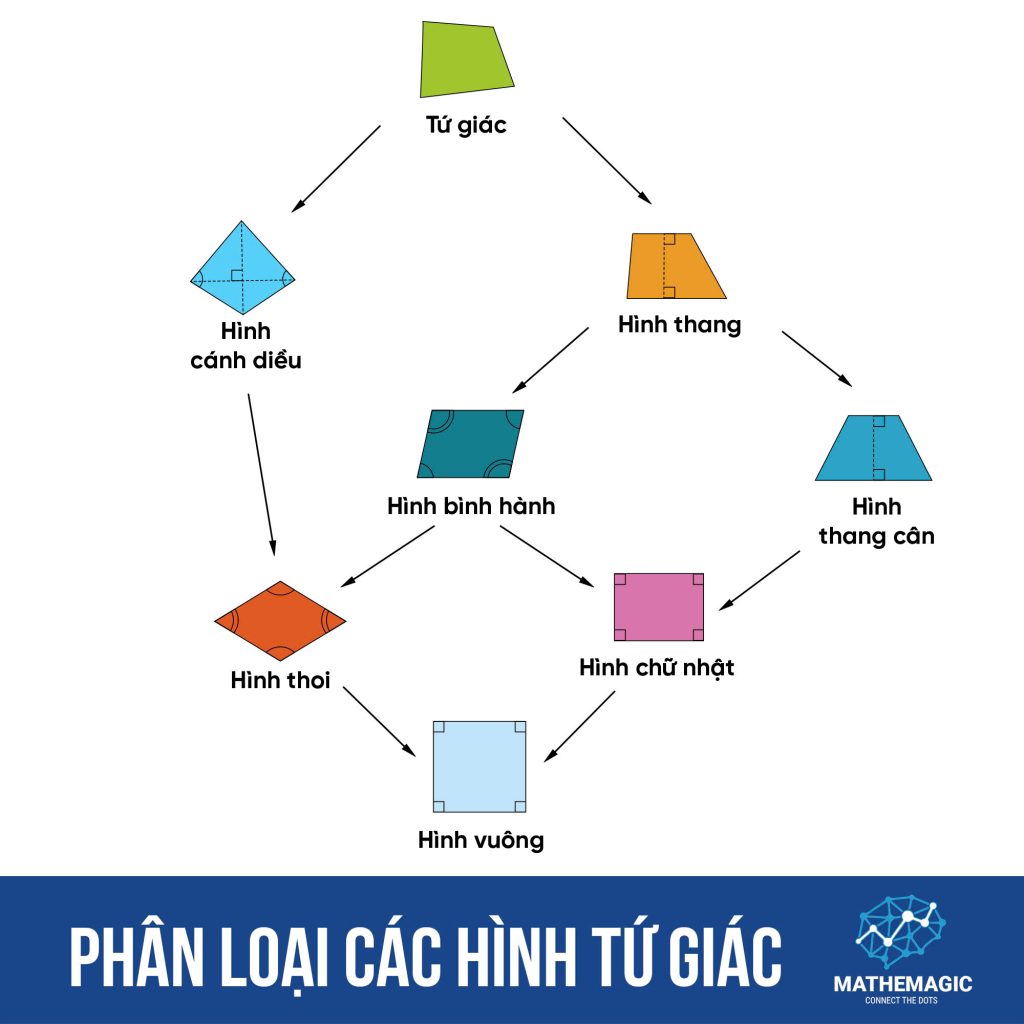
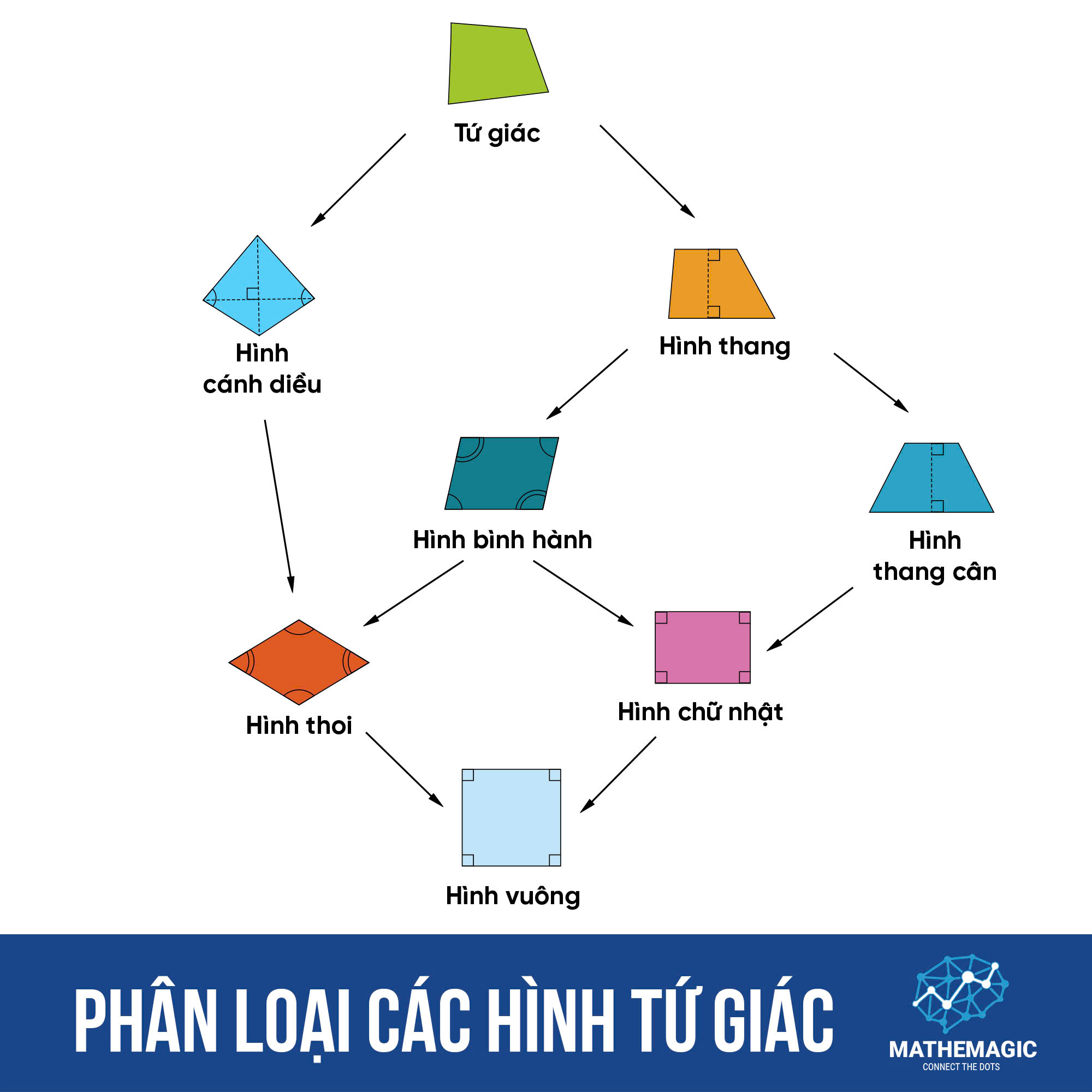
- Mối quan hệ giữa các Loại Tứ giác: Sơ đồ Tư duy
Trong sơ đồ, hình tứ giác bên dưới một hình tứ giác khác là trường hợp đặc biệt của hình đó.
Ví dụ, hình vuông là một hình chữ nhật đặc biệt, nhưng hình chữ nhật không phải là một hình vuông.
- Ứng dụng của Tứ giác trong Cuộc sống: Từ Xây dựng đến Nghệ thuật
Tứ giác có rất nhiều ứng dụng trong cuộc sống hàng ngày, từ xây dựng, kiến trúc đến nghệ thuật và thiết kế. Dưới đây là một số ví dụ:
- Xây dựng và kiến trúc: Tứ giác được sử dụng để xây dựng các tòa nhà, cầu đường, và các công trình kiến trúc khác.
- Nghệ thuật và thiết kế: Tứ giác được sử dụng trong hội họa, điêu khắc, và thiết kế đồ họa.
- Công nghệ: Tứ giác được sử dụng trong thiết kế màn hình máy tính, điện thoại, và các thiết bị điện tử khác.
- Toán học và khoa học: Tứ giác được sử dụng trong các bài toán hình học, vật lý, và các lĩnh vực khoa học khác.
- Bài tập và Hoạt động Thực hành: Củng cố Kiến thức
Để củng cố kiến thức về tứ giác, chúng ta có thể làm các bài tập và hoạt động thực hành sau:
- Vẽ các loại tứ giác khác nhau và xác định các đặc điểm và tính chất của chúng.
- Giải các bài toán liên quan đến tính diện tích và chu vi của tứ giác.
- Tìm kiếm các ví dụ về tứ giác trong cuộc sống hàng ngày.
- Thiết kế các mẫu hình tứ giác để trang trí.
Kết luận: Tứ giác – Viên gạch Vững chắc của Hình học Phẳng
Tứ giác là một hình đa giác cơ bản và quan trọng trong hình học phẳng. Việc nắm vững các khái niệm, đặc điểm và tính chất của tứ giác sẽ giúp chúng ta hiểu rõ hơn về thế giới hình học và ứng dụng chúng vào cuộc sống hàng ngày.